(287-212 B.c) Archimedes Grade Mathematician And Engineer, COMPLEMENTARY OF AUGUST 2007 Options

[Eua1]

ARCHIMEDES GRADE MATHEMATICIAN AND ENGINEER
(287-212 B.C)




Archimedes, the grader mathematician of ancient Greek world and the bigger mathematic intelligence of Europe up to the appearance of Newton, was given birth, lived and died at Syracuses, the big Greek colony of Sicily. His father was the astronomer Fidias, who had bonds of friendship with the royal gender of Syracuses. Archimedes travelled to Egypt and he came in contact with the successors of Euklidis, Eratosthenus and Dositheus, while he was friend and schoolmate of Konona the Samius. Like most scientists of his time, Archimedes was educated at the Museum in Alexandria, but unlike most, he did not stay in Alexandria. He returned to Syracuse, probably because of his kinship with Hieron II. Being a wealthy aristocrat, Archimedes had no need for the patronage of the Ptolemys. Many stories are told about Archimedes:
For example, he is supposed to have been so absent-minded that he often could not remember whether he had eaten.
Another (perhaps apocryphal) story has to do with the discovery of “Archimedes Principle” in hydrostatics. According to the story, Hieron had purchased a golden crown of complex shape, and he had begun to suspect that the goldsmith had cheated him by mixing silver with gold. Since Hieron knew that his bright relative, Archimedes, was an expert in calculating the volumes of complex shapes, he took the crown to Archimedes and asked him to determine whether it was made of pure gold (by calculating its specific gravity). However, the crown was too irregularly shaped, and even Archimedes could not calculate its volume.
While he was sitting in his bath worrying about this problem, Archimedes reflected on the fact that his body seemed less heavy when it was in the water. Suddenly, in a flash of intuition, he saw that the amount by which his weight was reduced was equal to the weight of the displaced water. He leaped out of his bath shouting “Eureka! Eureka!” (“I¢ve found it!”) and ran stark naked through the streets of Syracuse to the palace of Hieron to tell him of the discovery.
The story of Hieron¢s crown illustrates the difference between the Hellenistic period and the classical period. In the classical period, geometry was a branch of religion and philosophy. For aesthetic reasons, the tools which a classical geometer was allowed too use were restricted to a compass and a straight-edge. Within these restrictions, many problems are insoluble. For example, within the restrictions of classical geometry, it is impossible to solve the problem of trisecting an angle. In the story of Hieron¢s crown, Archimedes breaks free from the classical restrictions and shows himself willing to use every conceivable means to achieve his purpose.

One of Archimedes¢ great contributions to mathematics was his development of methods for finding the areas of plane figures bounded by curves, as well as methods for finding the areas and volumes of solid figures bounded by curved surfaces. To do this, he employed the “doctrine of limits”. For example, to find the area of a circle, he began by inscribing a square inside the circle. The area of the square was a first approximation to the area of the circle. Next, he inscribed a regular octagon and calculated its area, which was a closer approximation to the area of the circle. This was followed by a figure with 16 sides, and then 32 sides, and so on. Each increase in the number of sides brought him closer to the true area of the circle.
Archimedes also circumscribed polygons about the circle, and thus he obtained an upper limit for the area, as well as a lower limit. The true area was trapped between the two limits. In this way, Archimedes showed that the value of pi lies between 223/71 and 220/70. Sometimes Archimedes¢ use of the doctrine of limits led to exact results. For example, he was able to show that the ratio between the volume of a sphere inscribed in a cylinder to the volume of the cylinder is 2/3, and that the area of the sphere is 2/3 the area of the cylinder. He was so pleased with this result that he asked that a sphere and a cylinder be engraved on his tomb, together with the ratio, 2/3. Another problem which Archimedes was able to solve exactly was the problem of calculating the area of a plane figure bounded by a parabola. In his book On method, Archimedes says that it was his habit to begin working on a problem by thinking of a plane figure as being composed of a very large number of narrow strips, or, in the case of a solid, he thought of it as being built up from a very large number of slices. This is exactly the approach which is used in integral calculus.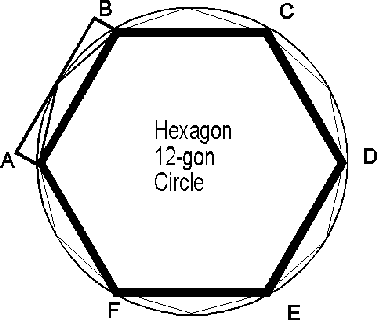



Archimedes must really be credited with the invention of both differential and integral calculus. He used what amounts to integral calculus to find the volumes and areas not only of spheres, cylinders and cones, but also of spherical segments, spheroids, hyperboloids and paraboloids of revolution; and his method for constructing tangents anticipates dif- ferential calculus.

Unfortunately, Archimedes was unable to transmit his invention of the calculus to the other mathematicians of his time. The difficulty was that there was not yet any such thing as algebraic geometry. The Pythagoreans had never recovered from the shock of discovering irrational numbers, and they had therefore abandoned algebra in favor of geometry. The union of algebra and geometry, and the development of a calculus which even non-geniuses could use, had to wait for Descartes, Fermat, Newton and Leibnitz.

Archimedes was the father of statics (as well as of hydrostatics). He calculated the centers of gravity of many kinds of figures, and he made a systematic, quantitative study of the properties of levers. He is supposed to have said: “Give me a place to stand on, and I can move the world!”
This brings us to another of the stories about Archimedes: According to the story, Hieron was a bit sceptical, and he challenged Archimedes to prove his statement by moving something rather enormous, although not necessarily as large as the world. Archimedes goodhumoredly accepted the challenge, hooked up a system of pulleys to a fully-loaded ship in the harbor, seated himself comfortably, and without excessive effort he singlehandedly pulled the ship out of the water and onto the shore.



Archimedes had a very compact notation for expressing large numbers. Essentially his system was the same as our own exponential notation, and it allowed him to handle very large numbers with great ease. In a curious little book called The Sand Reckoner, he used this notation to calculate the number of grains of sand which would be needed to fill the universe. (Of course, he had to make a crude guess about the size of the universe.) Archimedes wrote this little book to clarify the distinction between things which are very large but finite and things which are infinite. He wanted to show that nothing finite - not even the number of grains of sand needed to fill the universe - is too large to be measured and expressed in numbers. The Sand Reckoner is important as an historical document, because in it Archimedes incidentally mentions the revolutionary heliocentric model of Aristarchus, which does not occur in the one surviving book by Aristarchus himself.

In addition to his mathematical genius, Archimedes showed a superb mechanical intuition, similar to that of Leonardo da Vinci. Among his inventions are a planetarium and an elegant pump in the form of a helical tube. This type of pump is called the “screw of Archimedes”, and it is still in use in Egypt. The helix is held at an angle to the surface of the water, with its lower end half-immersed. When the helical tube is rotated about its long axis, the water is forced to flow uphill! His humanity and his towering intellect brought Archimedes universal respect, both during his own lifetime and ever since. However, he was not allowed to live out his life in peace; and the story of his death is both dramatic and symbolic



His work was enormous, so much qualitatively as much as quantitatively, and his inquiring glance covers a lot of sectors: geometry, catoptric, hydraulic, mechanic, architecture, besieging. He connected his name with the birth of the mechanic in ancient Greece and with the solution of eminent mathematic problems. Apart from all, his existence was mainly connected with the siege of his bornplace by the Romans. When finally the city was occupied by betrayal, the fable says that despite Marcellus' orders that Archimedes not be killed, a Roman soldier killed the famous scientist, while he was fixing in some mathematic problem. According to the fable one of them found Archimedes seated calmly in front of diagrams sketched in the sand, working on a mathematical problem. When the soldier ordered him to come along, the great mathematician is supposed to have looked up from his work and replied: "ìç ìïõ ôïõò êýêëïõò ôáñáôáé " (in free translation it means: "don't disturb my circles" or "don't disturb my thoughts"). The soldier immediately killed him.Archimedes was found in the coast, the moment that Romans landing at the coast of Syracuses and endered in the city, who was fixing on a problem with circles that he had formed on the sand.

Archimedes invented a lot of mechanisms that remained well-known in the history of the world of mechanics and technology, however his enormous work was not entire rescued, therefore many of these mechanisms cannot be described. His most significant mechanical inventions were: the aerometer-densitometer (without description), the astronomical device for the calculation of the size and the distance of the stars, weigthpull-hydroscope-intellectual (âáñýïõëêïò-õäñïóêïðßáé-ðíåõìáôéêÞ), instruments of attraction of weights and instruments that operated with air or steam, reflectors, with which heset on fire the roman fleet, the worm-screw or elix, the appliance for the pumping of water from the lower levels, the odometer-roadmeter (ïäüìåôñï-äñïìüìåôñï), appliance for measuring the distances, planetarium or ball (óöáßñá) which reconstructed the world, and in which was in repeated the movements of moon, sun, planets and the signs of the zodiac, pulley-block (ðïëýóðáóôïí), three-pulley-block (ôñéóðáóôïí), mechanisms for the lift of weights with ropes, sifon (óßöùí), “Stomachion”, the game of seesaw, hydraulic clock and cannon (ôçëåâüëï).


anemologio


hydroscope


dromometer


odometer


sifon

The mechanic Sakkas I. made the representation of the last mechanism in 1990, as also and that of the hydraulic clock and the lens. Archimedes influenced to a large extent the European thought , as well as the arabian scientists that copied all the work in the Arabics, language in which they were rescued quite a few since as the prototypes have been lost.

Source : [S.STAMATI, "ARHIMEDES¢ WORK" volume 4 Technical Chamber Greece, 1974
Bell, E.T. Men of Mathematics. New York: Simon and Schuster, Inc., 1937. pp. 28-34.
Lewis, Albert C. "Archimedes." Encyclopedia of World Biography. New York: McGraw-Hill, Inc., 1973. vol. 1, pp.219-223.
http://scidiv.bcc.ctc.edu/math/Archimedes.html

[Eua1]

The land forces were conducted by Appius Marcellus, with sixty galleys, each with five rows of oars, furnished with all sorts of arms and missiles, and a huge bridge of planks laid upon eight ships chained together, upon which was carried the engine to cast stones and darts, assaulted the walls, relying on the abundance and magnificence of his preparations, and on his own previous glory; all which, however, were, it would seem, but trifles for Archimedes and his machines.
These machines he had designed and contrived, not as matters of any importance, but as mere amusements in geometry; in compliance with king Hiero¢s desire and request, some little time before, that he should reduce to practice some part of his admirable speculations in science, and by accommodating the theoretic truth to sensation and ordinary use, bring it more within the appreciation of people in general.
...
When, therefore, the Romans assaulted the walls in two places at once, fear and consternation stupefied the Syracusans, believing that nothing was able to resist that violence and those forces. But when Archimedes began to ply his engines, he at once shot against the land forces all sorts of missile weapons, and immense masses of stone that came down with incredible noise and violence, against which no man could stand; for they knocked down those upon whom they fell, in heaps, breaking all their ranks and files. In the meantime huge poles thrust out from the walls over the ships, sunk some by the great weights which they let down from on high upon them; others they lifted up into the air by an iron hand or beak like a crane¢s beak, and, when they had drawn them up by the prow, and set them on end upon the ...., they plunged them to the bottom of the sea; or else the ships, drawn by engines within, and whirled about, were dashed against steep rocks that stood jutting out under the walls, with great destruction of the soldiers that were aboard them. A ship was frequently lifted up to a great height in the air (a dreadful thing to behold), and was rolled to and fro, and kept swinging, until the mariners were all thrown out, when at length it was dashed against the rocks, or let fall.

(Plutarch, Marcellus)

[Eua1]

Archimedes' principle
Archimedes' principle states that any body completely or partially submerged in a fluid is acted upon by an upward force which is equal to the weight of the fluid displaced by the body.

Archimedes' screw
Archimedes' screw consists of a pipe in the shape of a helix with its lower end dipped in the water. As the device is rotated the water rises up the pipe.

circumscribed
A circle is said to be circumscribed to a triangle or other polygon if the vertices of the polygon lie on the circle.
The polygon is than said to be inscribed in the circle.
The (unique) circle circumscribed to a triangle is called the circumcircle and its centre is the circumcentre.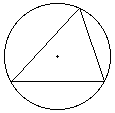


ellipse
A ellipse is one of the conic sections.
It may be defined using the focus directrix property as the locus of points whose distance from a fixed point is a fixed multiple e < 1 from a fixed line.
or via Cartesian coordinates as the set of points in a plane satisfying the equation :
ax2 + by2 = 1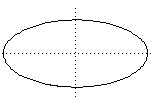


great circle
A great circle is a line of shortest distance on a sphere: the intersection of the sphere with a plane through the origin.

infinitesimal
An infinitesimal is an arbitrarily small quantity which early mathematicians found it necessary to incorporate into their theories in the absence of a proper theory of limits.
Infinitesimal calculus is the Differential and Integral Calculus.


method of exhaustion
The method of exhaustion is calculating an area by approximating it by the areas of a sequence of polygons.
For example, filling up the interior of a circle by inscribing polygons with more and more sides.

parabola
A parabola is one of the conic sections.
It may be defined using the focus directrix property as the locus of points which are equidistant from a fixed line and a fixed point.
or via Cartesian coordinates as the set of points in a plane satisfying the equation :
y = x2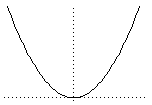


quadrature
Quadrature means calculating the area of a figure or the area under the graph of a function. Literally, finding a square with the same area.

tangent
A tangent to a curve at a point p is the best linear approximation to the curve near that point. It can be regarded as the limit of the chords from the point p to other points close to p.
If two curves have a common tangent at a point of intersection they are said to touch or be tangent.

[Eua1]

Other related links:


http://www-history.mcs.st-andrews.ac.uk/Ex...The_Method.html
http://www-history.mcs.st-andrews.ac.uk/Ex...s_parabola.html
http://www-history.mcs.st-andrews.ac.uk/Ex...on_statics.html

[NickTheGreek]

the forum missed topics like these !

[Big]

The most interesting topic i have ever read

I think that is better to have a translation of this document in Greek for people who doesn't know English.

[Eua1]

The most interesting topic i have ever read

I think that is better to have a translation of this document in Greek for people who doesn't know English.

You must believe me when I say that such posts is much more easier for me to do it in greek language than in english ...

If you, guys, believe that they must be in greek language too, so be it.....I will try to

sorry guys...... I didn't thanked you, did I???? so